Cross-sectional Parameterization and Beam Properties

The cross-section is comprised of the following components: box spar, front laminate, back laminate, front filling, back filling and non-structural mass, as shown in Fig. 3.

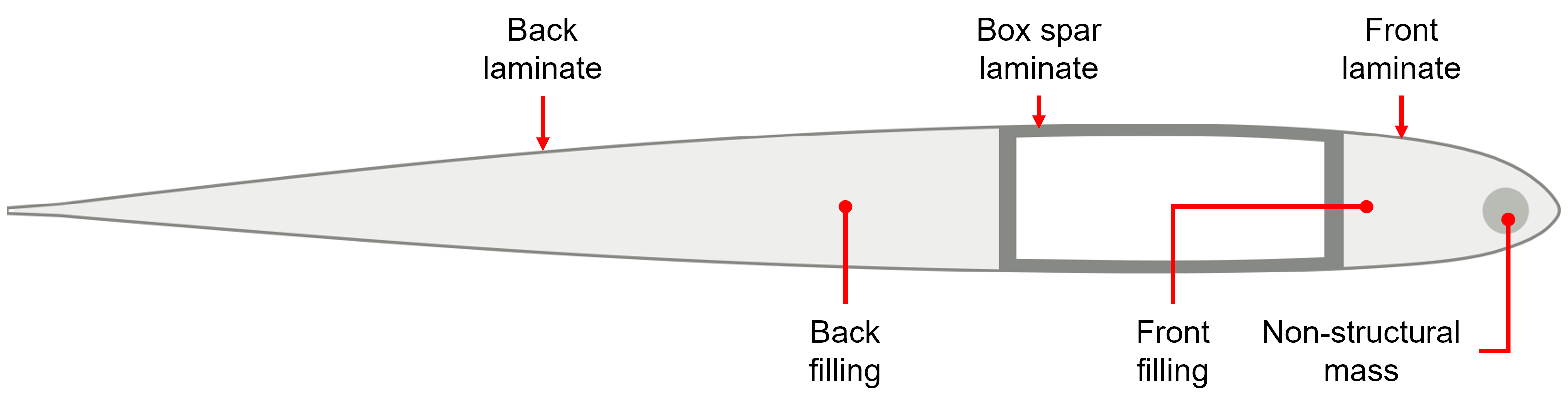
Figure 3 Components of the cross-section.

Parameterization

Parameters can be in general grouped into two sets, geometry related and layup related.

Geometry

In this example, four geometric parameters are defined in the non-dimensional frame where the chord length is 1, as shown in Fig. 4. The origin of this frame is placed at the leading edge. The size and location of the box spar are defined by the two parameters \(a_2^{wl}\) and \(a_2^{wt}\), which are in fact the horizontal coordinates of the leading and trailing webs, respectively. The non-structural mass is assumed to be a circular object in this example. Hence, the three parameters defining the size and location are the horizontal coordinate \(a_2^{nsm}\) and vertical coordinate \(a_3^{nsm}\) of the center, and the radius \(r^{nsm}\).

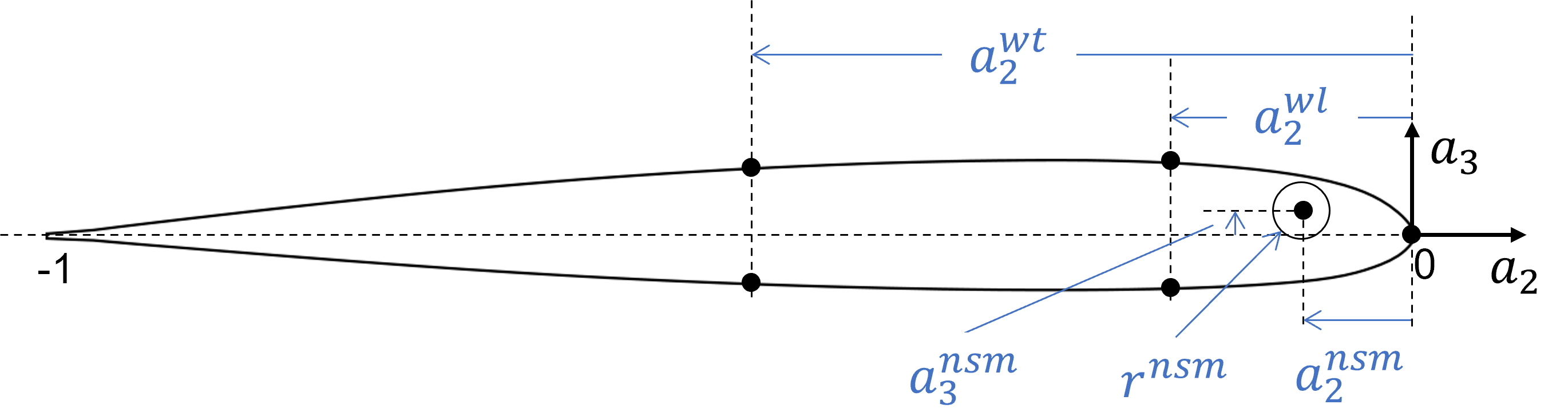
Figure 4 Parameters for the geometry in the non-dimensional frame, where the chord length is 1.

Layup

Layup related parameters are used to define materials (\(l\)), fiber angles (\(\theta\)) and numbers of plies (\(n\)) for the laminates of box spar, cap and overwrap. In this example, the box spar laminate is assumed to have four layers. All four layers have the same material (\(l^s\)), but can have different fiber angles (\(\theta_1^s, \theta_2^s, \theta_3^s, \theta_4^s\)) and numbers of plies (\(n_1^s, n_2^s, n_3^s, n_4^s\)). The cap laminate is assumed to have a single layer with three parameters: \(l^c, \theta^c, n^c\). The overwrap laminate is also assumed having a single layer with three parameters: \(l^o, \theta^o, n^o\).

The overall layup design of the three lamiante components are listed in Table 4, Table 5 and Table 6.

Table 4 Layup of the box spar laminate

Layer	Lamina	Fiber angle [deg]	Ply count
Base	T300 15k/976	0	2
1	\(l^s\)	\(\theta^s_1\)	\(n^s_1\)
2	\(l^s\)	\(\theta^s_2\)	\(n^s_2\)
3	\(l^s\)	\(\theta^s_3\)	\(n^s_3\)
4	\(l^s\)	\(\theta^s_4\)	\(n^s_4\)

Table 5 Layup of the front laminate

Layer	Lamina	Fiber angle [deg]	Ply count
Cap	Aluminum 8009	0	2
Base	T300 15k/976	0	2
1	\(l^f\)	\(\theta^f\)	\(n^f\)

Table 6 Layup of the back laminate

Layer	Lamina	Fiber angle [deg]	Ply count
Base	T300 15k/976	0	2
1	\(l^b\)	\(\theta^b\)	\(n^b\)

A summary of the parameters is listed in Table 7.

Table 7 Summary of parameters

Symbol	Name in input files	Description
\(a_2^{wl}\)	wl_a2	Non-dimensional horizontal coordinate of the leading web of the box spar
\(a_2^{wt}\)	wt_a2	Non-dimensional horizontal coordinate of the trailing web of the box spar
\(a_2^{nsm}\)	pnsmc_a2	Non-dimensional horizontal coordinate of the center of the non-structural mass
\(a_3^{nsm}\)	pnsmc_a3	Non-dimensional vertical coordinate of the center of the non-structural mass
\(r^{nsm}\)	nsmr	Non-dimensional radius of the non-structural mass
\(l^s\)	mi_spar_1	Material (lamina) selection of the box spar layup
\(\theta_1^s\)	fo_spar_1	Fiber angle of layer 1 of the box spar layup
\(\theta_2^s\)	fo_spar_2	Fiber angle of layer 2 of the box spar layup
\(\theta_3^s\)	fo_spar_3	Fiber angle of layer 3 of the box spar layup
\(\theta_4^s\)	fo_spar_4	Fiber angle of layer 4 of the box spar layup
\(n_1^s\)	np_spar_1	Number of plies of layer 1 of the box spar layup
\(n_2^s\)	np_spar_2	Number of plies of layer 2 of the box spar layup
\(n_3^s\)	np_spar_3	Number of plies of layer 3 of the box spar layup
\(n_4^s\)	np_spar_4	Number of plies of layer 4 of the box spar layup
\(l^c\)	mi_le	Material (lamina) selection of the cap layup
\(\theta^c\)	fo_le	Fiber angle of the cap layup
\(n^c\)	np_le	Number of plies of the cap layup
\(l^o\)	mi_te	Material (lamina) selection of the overwrap layup
\(\theta^o\)	fo_te	Fiber angle of the overwrap layup
\(n^o\)	np_te	Number of plies of the overwrap layup

Some other parameters used are listed below:

Table 8 Summary of other parameters

Name in input files	Description
chord	Chord length of the cross-section
oa2	Non-dimensional horizontal coordinate of the origin of the frame \(\mathbf{x}\) used in VABS.
pfte2_a2	Non-dimensional location of point marking the coarse meshes in the filling region
mesh_size	Global mesh size
mesh_size_fill	Mesh size for the filling regions

Materials

Materials used in this example are summarized in Table 9. Lamina thickness is given in Table 10. ‘Aluminum 80009’ is used as the outermost layer of the cap. ‘Lead’ is used for the non-structural mass. ‘Rohacell 70’ is used at the leading filling region. ‘Plascore PN2-3/16OX3.0’ is used at the trailing filling region. ‘T300 15k/976’ is used as the base layer for the spar, cap and overwrap, to prevent zero layers during the optimization. The last four rows in the table are the candidate materials for the layup design of the three components.

Table 9 Material properties

Material	Density	\(E_1\)	\(E_2\)	\(E_3\)	\(\nu_{12}\)	\(\nu_{13}\)	\(\nu_{23}\)	\(G_{12}\)	\(G_{13}\)	\(G_{23}\)
	[\(\mathrm{lbf\cdot s^2/in^4}\)]	[\(\mathrm{psi}\)]	[\(\mathrm{psi}\)]	[\(\mathrm{psi}\)]				[\(\mathrm{psi}\)]	[\(\mathrm{psi}\)]	[\(\mathrm{psi}\)]
Aluminum 8009	\(0.271959\times 10^{-3}\)	\(13.1\times 10^6\)			\(0.33\)
Lead	\(1.060957\times 10^{-3}\)	\(1.0\times 10^{-3}\)			\(0\)
Rohacell 70	\(7.040895\times 10^{-6}\)	\(13.125\times 10^3\)	\(13.125\times 10^3\)	\(13.125\times 10^3\)	\(0.315\)	\(0.315\)	\(0.300\)	\(4.118\times 10^3\)	\(4.118\times 10^3\)	\(4.118\times 10^3\)
Plascore PN2-3/16OX3.0	\(4.509066\times 10^{-6}\)	\(1.0\times 10^3\)	\(1.0\times 10^3\)	\(20\times 10^3\)	\(0.30\)	\(0.01\)	\(0.01\)	\(1.0\times 10^3\)	\(3.5\times 10^3\)	\(5.799\times 10^3\)
T300 15k/976	\(0.149716\times 10^{-3}\)	\(19.6\times 10^6\)	\(1.34\times 10^6\)		\(0.348\)			\(0.91\times 10^6\)
AS4 12k/E7K8	\(0.145973\times 10^{-3}\)	\(19.3\times 10^6\)	\(1.23\times 10^6\)		\(0.32\)			\(7.31\times 10^6\)
S2/SP381	\(0.173109\times 10^{-3}\)	\(7.05\times 10^6\)	\(1.97\times 10^6\)		\(0.263\)			\(0.59\times 10^6\)
T650-35 12k/976	\(0.148781\times 10^{-3}\)	\(22.0\times 10^6\)	\(1.30\times 10^6\)		\(0.115\)			\(0.745\times 10^6\)
T700 24K/E765	\(0.145037\times 10^{-3}\)	\(18.71\times 10^6\)	\(1.36\times 10^6\)		\(0.319\)			\(0.65\times 10^6\)

Table 10 Lamina thickness

Material	Thickness [\(in\)]
Aluminum 8009	0.01
T300 15k/976	0.0053
AS4 12k/E7K8	0.0054
S2/SP381	0.0092
T650-35 12k/976	0.0052
T700 24K/E765	0.0056

Properties

The beam properties calculated by VABS listed in Table 11 will be needed in the optimization. Fig. 5 shows the points and axes with respect to which some properties are calculated. The two bending stiffnesses are given with respect to the principal bending axes. The horizontal locations of the shear and mass centers are given with respect to the modeling origin, which is the quarder chord in this example.

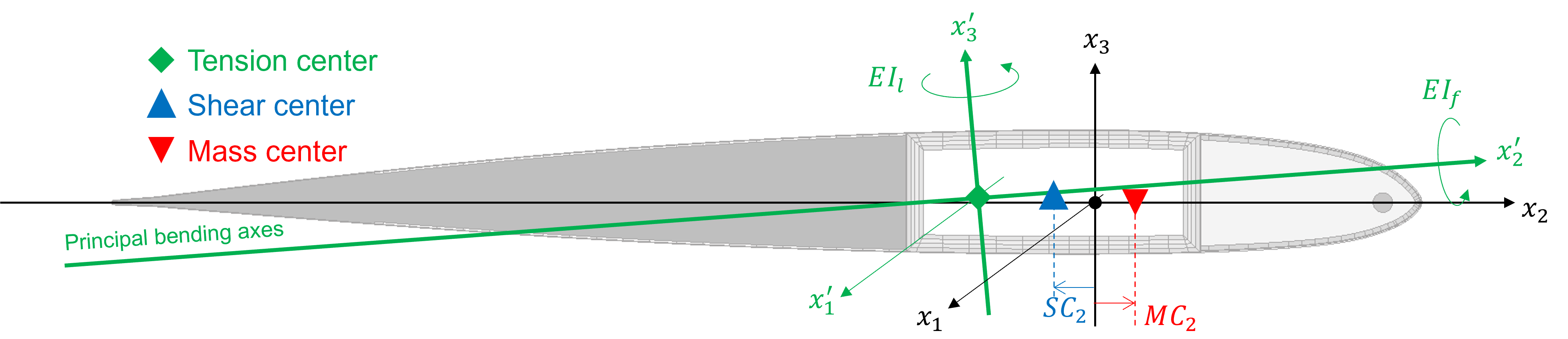
Figure 5 Beam properties and their reference of calculation.

A summary of the properties is listed in Table 11.

Table 11 Summary of properties

Symbol	Name in input files	Description
\(m\)	mu	Mass per unit length
\(GJ\)	gj	Torsional stiffness
\(EI_f\)	ei22	Flapping bending stiffness
\(EI_l\)	ei33	Lead-lag bending stiffness
\(SC_2\)	sc2	Horizontal coordinate of the shear center in the frame x.
\(MC_2\)	mc2	Horizontal coordinate of the mass center in the frame x.