Channel

Problem description

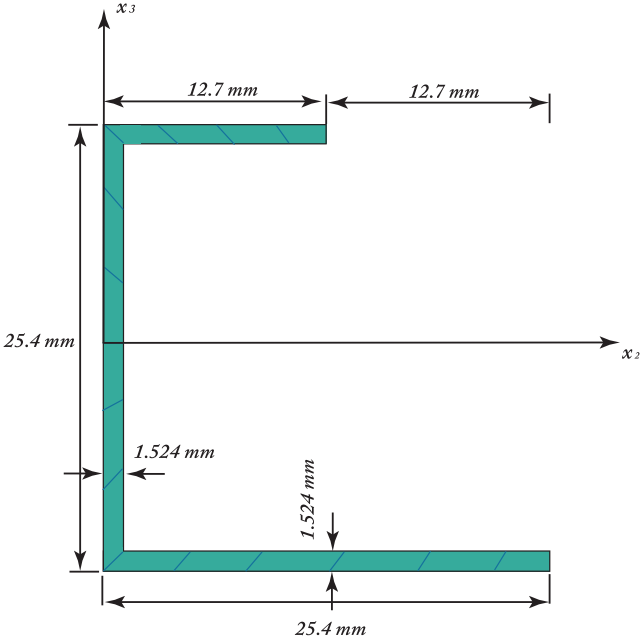
Figure 56 Cross section of the pipe [CHEN2010].

This example has a cross section of a highly heterogeneous channel. This cross section geometry can be defined as shown in Fig. 56 [CHEN2010]. The isotropic material properties are given in Table 50. The layup is defined having a single layer with the thickness 0.001524 m. The result is shown in Table 52 and compared with those in [CHEN2010]. Complete input files can be found in examples\ex_channel\, including channel.xml and materials.xml.

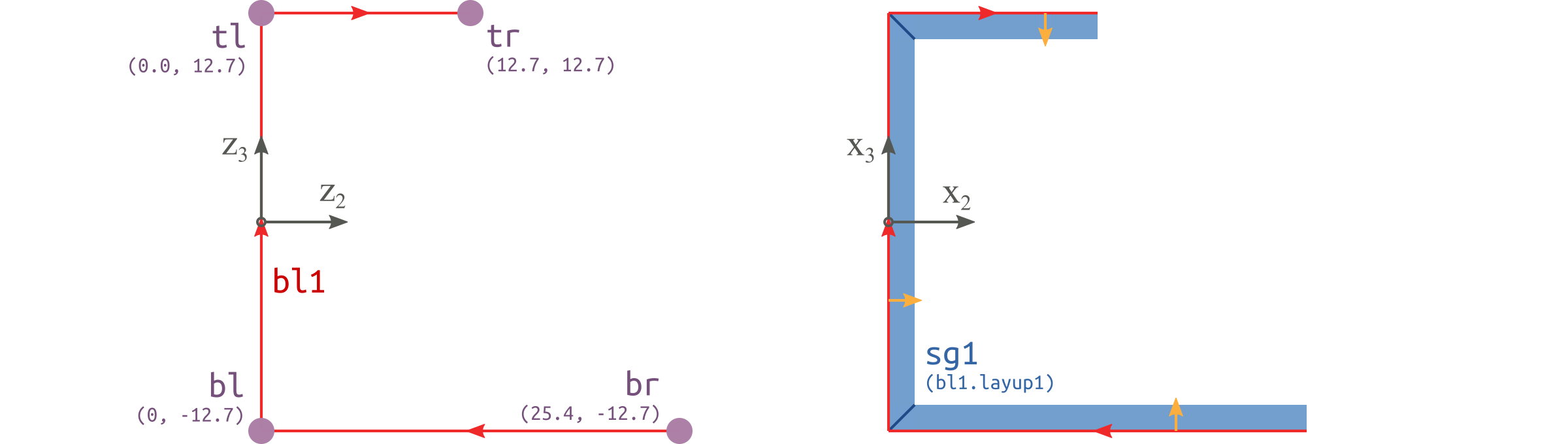
Figure 57 Base points, Base lines and Segments of the channel cross section.

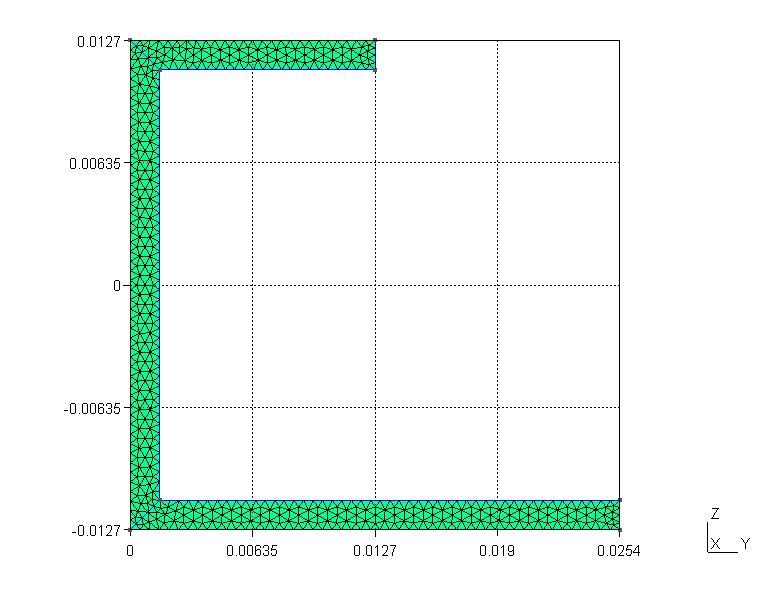
Figure 58 Meshed cross section viewed in Gmsh.

Table 50 Material properties

Name	Type	Density	\(E\)	\(\nu\)
		\(\mathrm{kg/m^3}\)	\(\mathrm{GPa}\)
mtr1	isotropic	1068.69	206.843	0.49

Table 51 Layups

Name	Layer	Material	Ply thickness	Orientation	Number of plies
			\(\mathrm{m}\)	\(\circ\)
layup1	1	mtr1	0.001524	0	1

Result

Table 52 Results

\(\phantom{-}1.906\times 10^7\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(-4.779\times 10^4\)	\(-1.325\times 10^5\)
\(\phantom{-}0.0\)	\(2.804\times 10^6\)	\(\phantom{-}2.417\times 10^5\)	\(\phantom{-}2.128\times 10^4\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(\phantom{-}0.0\)	\(2.417\times 10^5\)	\(\phantom{-}2.146\times 10^6\)	\(-7.663\times 10^3\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(\phantom{-}0.0\)	\(2.128\times 10^4\)	\(-7.663\times 10^3\)	\(\phantom{-}2.091\times 10^2\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(-4.779\times 10^4\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}2.011\times 10^3\)	\(\phantom{-}9.104\times 10^2\)
\(-1.325\times 10^5\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}9.104\times 10^2\)	\(\phantom{-}1.946\times 10^3\)

Table 53 Results from reference [CHEN2010]

\(\phantom{-}1.903\times 10^7\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(-4.778\times 10^4\)	\(-1.325\times 10^5\)
\(\phantom{-}0.0\)	\(2.791\times 10^6\)	\(\phantom{-}2.364\times 10^5\)	\(\phantom{-}2.122\times 10^4\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(\phantom{-}0.0\)	\(2.364\times 10^5\)	\(\phantom{-}2.137\times 10^6\)	\(-7.679\times 10^3\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(\phantom{-}0.0\)	\(2.122\times 10^4\)	\(-7.679\times 10^3\)	\(\phantom{-}2.086\times 10^2\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)
\(-4.778\times 10^4\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}2.010\times 10^3\)	\(\phantom{-}9.102\times 10^2\)
\(-1.325\times 10^5\)	\(0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}0.0\)	\(\phantom{-}9.102\times 10^2\)	\(\phantom{-}1.944\times 10^3\)