Circular tube

Problem description

This example has a cross section of a simple circular shape with radius \(r=10\) m. This cross section geometry can be defined easily by a center and a radius. Material properties are given in Table 47. The layup is defined using the stacking sequence code \([\pm 45_2/0_2/90]_{2s}\). The result is given in Table 49. Complete input files can be found in examples\ex_tube\, including tube.xml and materials.xml.

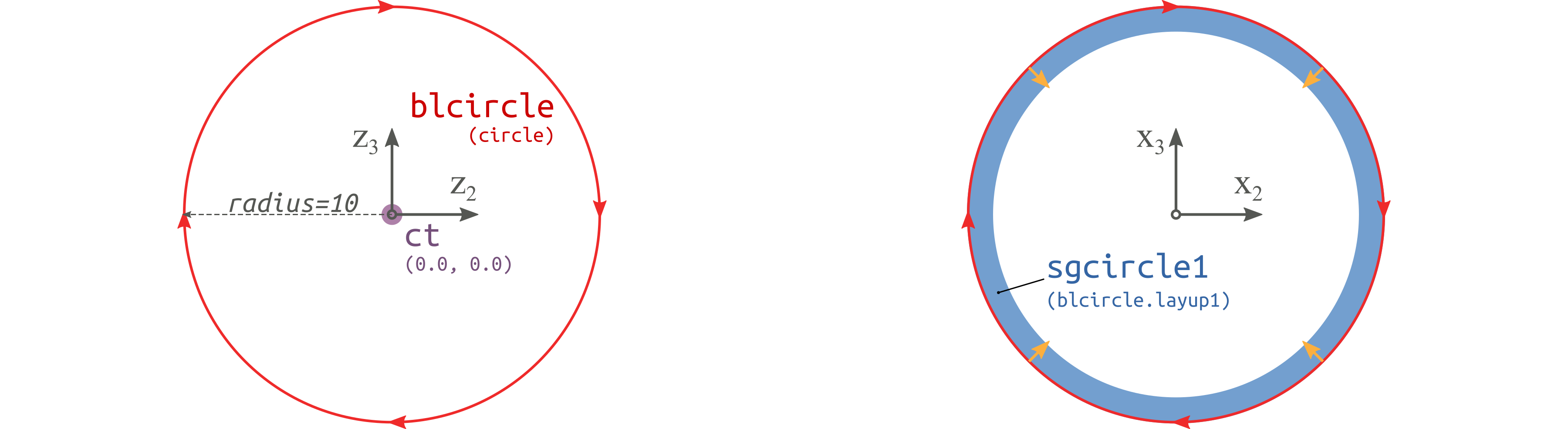
Figure 54 Base points, Base lines and Segments of the tube cross section.

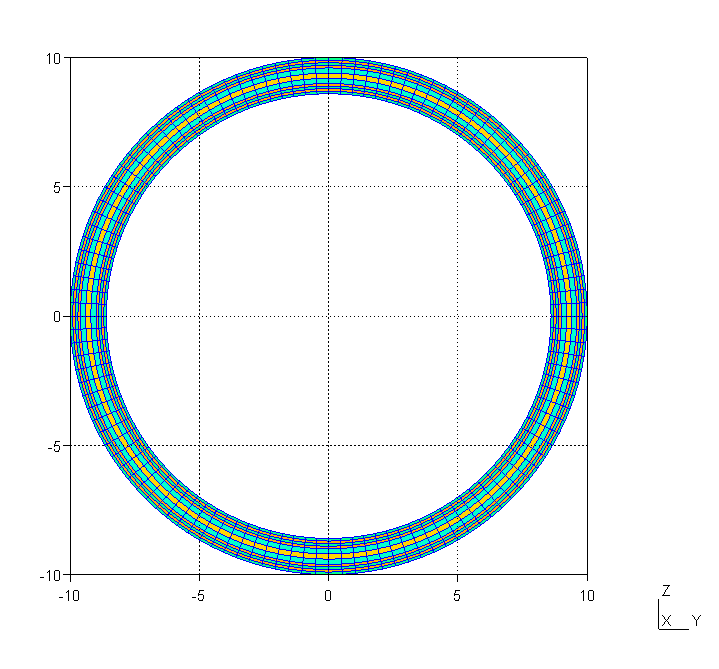
Figure 55 Meshed cross section viewed in Gmsh.

Table 47 Material properties

Name	Type	Density	\(E_{1}\)	\(E_{2}\)	\(E_{3}\)	\(G_{12}\)	\(G_{13}\)	\(G_{23}\)	\(\nu_{12}\)	\(\nu_{13}\)	\(\nu_{23}\)
		\(10^3\ \mathrm{kg/m^3}\)	\(\mathrm{GPa}\)	\(\mathrm{GPa}\)	\(\mathrm{GPa}\)	\(\mathrm{GPa}\)	\(\mathrm{GPa}\)	\(\mathrm{GPa}\)
iso5_4	orthotropic	1.664	10.3	10.3	10.3	8.0	8.0	8.0	0.3	0.3	0.3

Table 48 Layups

Name	Material	Stacking sequence
layup1	iso5_4	\([\pm 45_2/0_2/90]_{s}\)

Result

Table 49 Results

\(\phantom{-}1.108\times 10^{12}\)	\(-2.677\times 10^{-3}\)	\(-1.050\times 10^{-4}\)	\(-5.795\times 10^{-5}\)	\(-2.099\times 10^5\)	\(-1.626\times 10^5\)
\(-2.677\times 10^{-3}\)	\(\phantom{-}2.352\times 10^{11}\)	\(-1.583\times 10^3\)	\(\phantom{-}4.781\times 10^4\)	\(\phantom{-}3.200\times 10^{-3}\)	\(\phantom{-}2.063\times 10^{-2}\)
\(-1.050\times 10^{-4}\)	\(-1.583\times 10^3\)	\(\phantom{-}2.352\times 10^{11}\)	\(\phantom{-}4.086\times 10^4\)	\(\phantom{-}6.546\times 10^{-4}\)	\(\phantom{-}1.063\times 10^{-3}\)
\(-5.795\times 10^{-5}\)	\(\phantom{-}4.781\times 10^4\)	\(\phantom{-}4.086\times 10^4\)	\(\phantom{-}4.043\times 10^{13}\)	\(\phantom{-}2.717\times 10^{-7}\)	\(\phantom{-}3.229\times 10^{-8}\)
\(-2.099\times 10^5\)	\(\phantom{-}3.200\times 10^{-3}\)	\(\phantom{-}6.546\times 10^{-4}\)	\(\phantom{-}2.717\times 10^{-7}\)	\(\phantom{-}4.819\times 10^{13}\)	\(-1.399\times 10^6\)
\(-1.626\times 10^5\)	\(\phantom{-}2.063\times 10^{-2}\)	\(\phantom{-}1.063\times 10^{-3}\)	\(\phantom{-}3.229\times 10^{-8}\)	\(-1.399\times 10^6\)	\(\phantom{-}4.819\times 10^{13}\)