Beam Properties

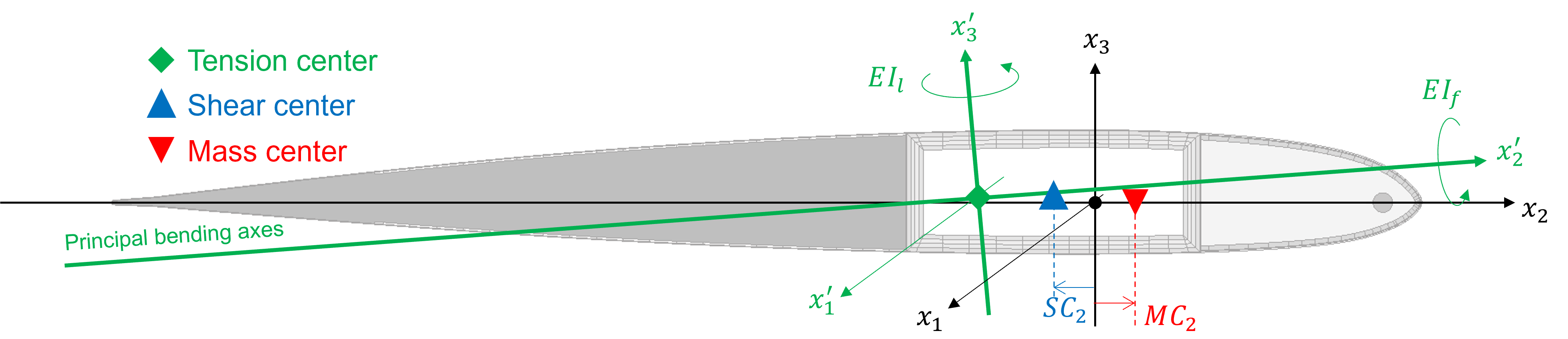
Figure 11 Reference frames of beam properties.

Inertial properties

Table 4 Inertial properties

Keyword	Description
mu	Mass per unit length
mmoi1 | mmoi2 | mmoi3	Mass moment of inertia about x1/x2/x3 axis
msijo (i, j are numbers 1 to 6)	Entry (i, j) of the 6x6 mass matrix at the origin
msijc (i, j are numbers 1 to 6)	Entry (i, j) of the 6x6 mass matrix at the mass center
mcy | mc2	y (or x2) component of the mass center
mcz | mc3	z (or x3) component of the mass center

\[\begin{split}\begin{bmatrix} \mu & 0 & 0 & 0 & \mu x_{M3} & -\mu x_{M2} \\ 0 & \mu & 0 & -\mu x_{M3} & 0 & 0 \\ 0 & 0 & \mu & \mu x_{M2} & 0 & 0 \\ 0 & -\mu x_{M3} & \mu x_{M2} & i_{22}+i_{33} & 0 & 0 \\ \mu x_{M3} & 0 & 0 & 0 & i_{22} & i_{23} \\ -\mu x_{M2} & 0 & 0 & 0 & i_{23} & i_{33} \end{bmatrix}\end{split}\]

Stiffness properties

Table 5 Stiffness properties

Keyword	Description
ea	Axial stiffness
gj	Torsional stiffness
eiyy | ei22	Principal bending stiffness around the \(y\) (\(x_2\)) axis (flapwise)
eizz | ei33	Principal bending stiffness around the \(z\) (\(x_3\)) axis (chordwise or lead-lag)
gayy | ga22	Principal shear stiffness in along the \(y\) (\(x_2\)) axis
gazz | ga33	Principal shear stiffness in along the \(z\) (\(x_3\)) axis
stfijc (i, j are numbers 1 to 4)	Entry (i, j) of the 4x4 classical stiffness matrix (\(C^b_{ij}\))
stfijr (i, j are numbers 1 to 6)	Entry (i, j) of the 6x6 refined stiffness matrix (\(C^b_{ij}\))
cmpijc (i, j are numbers 1 to 4)	Entry (i, j) of the 4x4 classical compliance matrix (\(S^b_{ij}\))
cmpijr (i, j are numbers 1 to 6)	Entry (i, j) of the 6x6 refined compliance matrix (\(S^b_{ij}\))
tcy | tc2	\(y\) (\(x_2\)) component of the tension center
tcz | tc3	\(z\) (\(x_3\)) component of the tension center
scy | sc2	\(y\) (\(x_2\)) component of the shear center
scz | sc3	\(z\) (\(x_3\)) component of the shear center

Constitutive relation of the Euler-Bernoulli beam model:

\[\begin{split}\begin{Bmatrix} F_1 \\ M_1 \\ M_2 \\ M_3 \end{Bmatrix} = \begin{bmatrix} C^b_{11} & C^b_{12} & C^b_{13} & C^b_{14} \\ C^b_{12} & C^b_{22} & C^b_{23} & C^b_{24} \\ C^b_{13} & C^b_{23} & C^b_{33} & C^b_{34} \\ C^b_{14} & C^b_{24} & C^b_{34} & C^b_{44} \end{bmatrix} \begin{Bmatrix} \gamma_{11} \\ \kappa_{11} \\ \kappa_{12} \\ \kappa_{13} \end{Bmatrix}\end{split}\]

\[\begin{split}\begin{Bmatrix} \gamma_{11} \\ \kappa_{11} \\ \kappa_{12} \\ \kappa_{13} \end{Bmatrix} = \begin{bmatrix} S^b_{11} & S^b_{12} & S^b_{13} & S^b_{14} \\ S^b_{12} & S^b_{22} & S^b_{23} & S^b_{24} \\ S^b_{13} & S^b_{23} & S^b_{33} & S^b_{34} \\ S^b_{14} & S^b_{24} & S^b_{34} & S^b_{44} \end{bmatrix} \begin{Bmatrix} F_1 \\ M_1 \\ M_2 \\ M_3 \end{Bmatrix}\end{split}\]

Constitutive relation of the Timoshenko beam model:

\[\begin{split}\begin{Bmatrix} F_1 \\ F_2 \\ F_3 \\ M_1 \\ M_2 \\ M_3 \end{Bmatrix} = \begin{bmatrix} C^b_{11} & C^b_{12} & C^b_{13} & C^b_{14} & C^b_{15} & C^b_{16} \\ C^b_{12} & C^b_{22} & C^b_{23} & C^b_{24} & C^b_{25} & C^b_{26} \\ C^b_{13} & C^b_{23} & C^b_{33} & C^b_{34} & C^b_{35} & C^b_{36} \\ C^b_{14} & C^b_{24} & C^b_{34} & C^b_{44} & C^b_{45} & C^b_{46} \\ C^b_{15} & C^b_{25} & C^b_{35} & C^b_{45} & C^b_{55} & C^b_{56} \\ C^b_{16} & C^b_{26} & C^b_{36} & C^b_{46} & C^b_{56} & C^b_{66} \\ \end{bmatrix} \begin{Bmatrix} \gamma_{11} \\ \gamma_{12} \\ \gamma_{13} \\ \kappa_{11} \\ \kappa_{12} \\ \kappa_{13} \end{Bmatrix}\end{split}\]

\[\begin{split}\begin{Bmatrix} \gamma_{11} \\ \gamma_{12} \\ \gamma_{13} \\ \kappa_{11} \\ \kappa_{12} \\ \kappa_{13} \end{Bmatrix} = \begin{bmatrix} S^b_{11} & S^b_{12} & S^b_{13} & S^b_{14} & S^b_{15} & S^b_{16} \\ S^b_{12} & S^b_{22} & S^b_{23} & S^b_{24} & S^b_{25} & S^b_{26} \\ S^b_{13} & S^b_{23} & S^b_{33} & S^b_{34} & S^b_{35} & S^b_{36} \\ S^b_{14} & S^b_{24} & S^b_{34} & S^b_{44} & S^b_{45} & S^b_{46} \\ S^b_{15} & S^b_{25} & S^b_{35} & S^b_{45} & S^b_{55} & S^b_{56} \\ S^b_{16} & S^b_{26} & S^b_{36} & S^b_{46} & S^b_{56} & S^b_{66} \\ \end{bmatrix} \begin{Bmatrix} F_1 \\ F_2 \\ F_3 \\ M_1 \\ M_2 \\ M_3 \end{Bmatrix}\end{split}\]