Box beam

Problem description

Figure 38 Cross section of the box beam [YU2012].

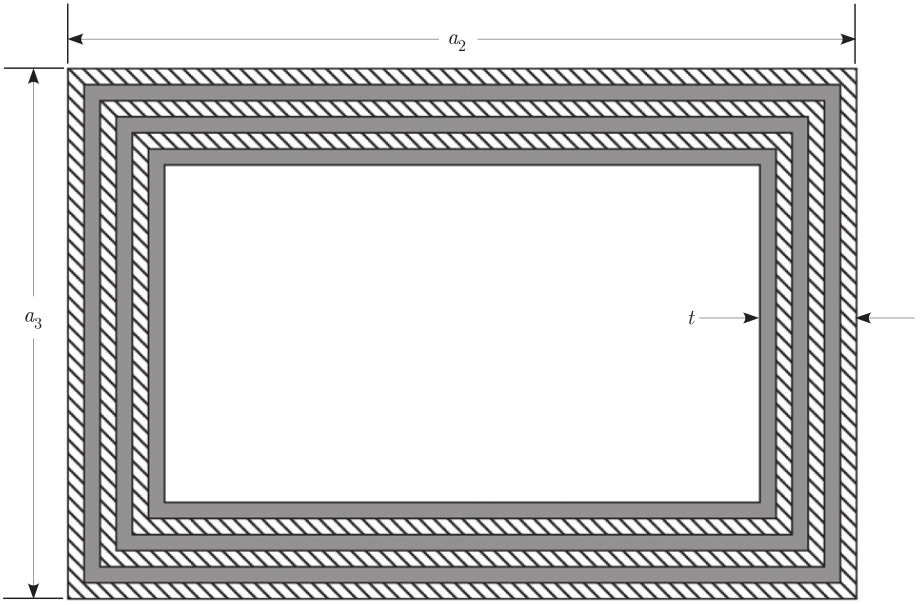
This example is a thin-walled box beam whose cross section is depicted in Fig. 38 [YU2012]. The width \(a_2=0.953\) in, height \(a_3=0.530\) in, and thickness \(t=0.030\) in. Each wall has six plies of the same composite material and the same fiber orientation of \(15^\circ\). Material properties and layup scheme are listed in Table 14 and Table 15. Cross-sectional properties are given in Table 16 and compared with those in Ref. [YU2012]. The tiny differences are due to different meshes. Complete input files can be found in examples\ex_box\, including box.xml and materials.xml.

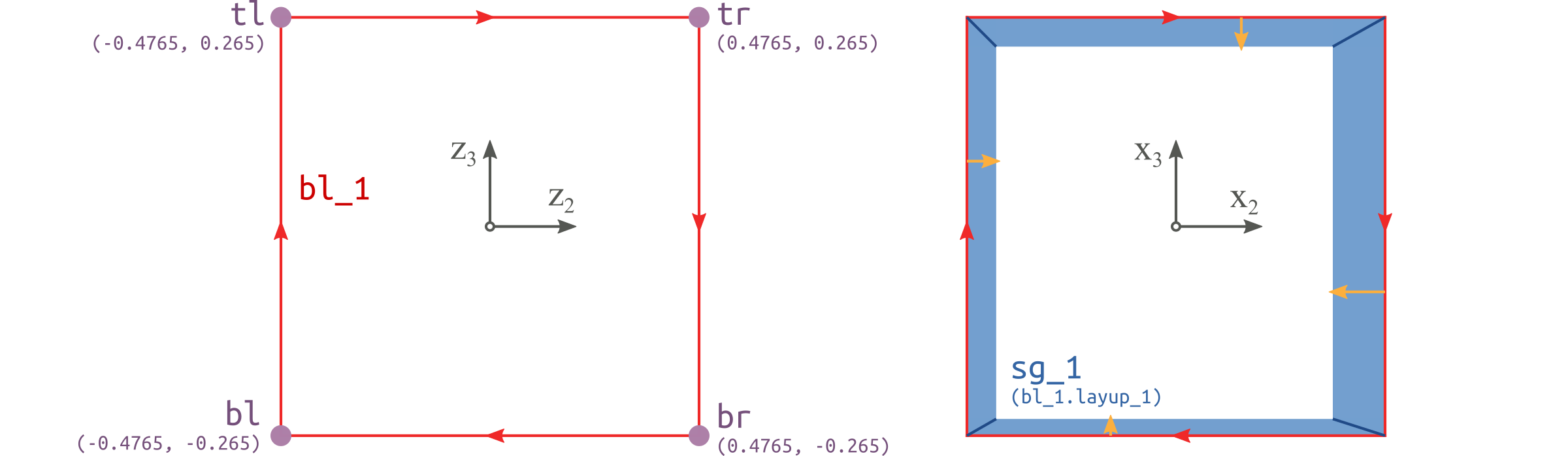
Figure 39 Base points, Base lines and Segments of the box beam cross section.

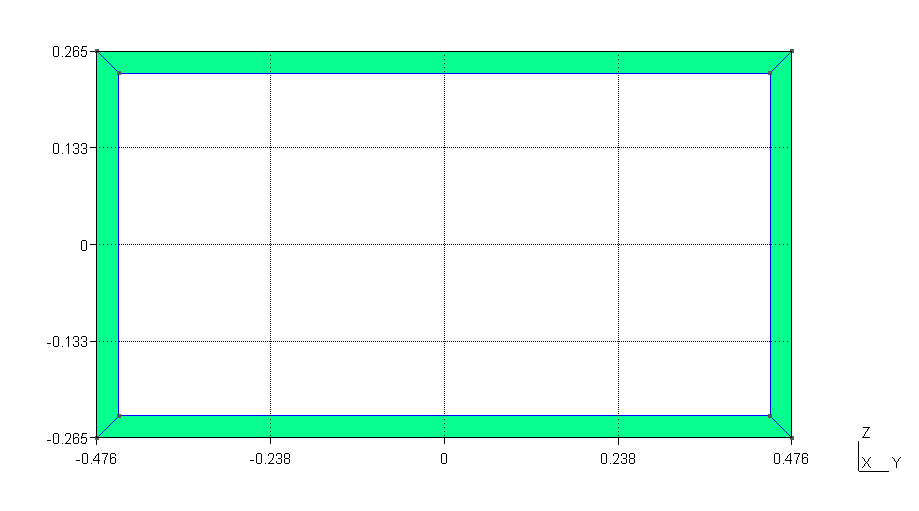
Figure 40 Meshed cross section viewed in Gmsh.

Table 14 Material properties

Name	Density	\(E_{1}\)	\(E_{2}\)	\(E_{3}\)	\(G_{12}\)	\(G_{13}\)	\(G_{23}\)	\(\nu_{12}\)	\(\nu_{13}\)	\(\nu_{23}\)
	\(\mathrm{lb\cdot sec^2/in^4}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)
mat_1	0.0001353	20.59	1.42	1.42	0.87	0.87	0.696	0.30	0.30	0.34

Table 15 Layups

Name	Layer	Material	Ply thickness	Orientation	Number of plies
			\(\mathrm{in}\)	\(\circ\)
layup1	1	mat_1	0.05	-15	6

Result

Table 16 Results

Component	Value	Reference [YU2012]
\(S_{11}\) [\(\mathrm{lbf}\)]	\(\phantom{-}1.437 \times 10^6\)	\(\phantom{-}1.437 \times 10^6\)
\(S_{22}\) [\(\mathrm{lbf}\)]	\(\phantom{-}9.026 \times 10^4\)	\(\phantom{-}9.027 \times 10^4\)
\(S_{33}\) [\(\mathrm{lbf}\)]	\(\phantom{-}3.941 \times 10^4\)	\(\phantom{-}3.943 \times 10^4\)
\(S_{14}\) [\(\mathrm{lbf \cdot in}\)]	\(\phantom{-}1.074 \times 10^5\)	\(\phantom{-}1.074 \times 10^5\)
\(S_{25}\) [\(\mathrm{lbf \cdot in}\)]	\(-5.201 \times 10^4\)	\(-5.201 \times 10^4\)
\(S_{36}\) [\(\mathrm{lbf \cdot in}\)]	\(-5.635 \times 10^4\)	\(-5.635 \times 10^4\)
\(S_{44}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}1.679 \times 10^4\)	\(\phantom{-}1.679 \times 10^4\)
\(S_{55}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}6.621 \times 10^4\)	\(\phantom{-}6.621 \times 10^4\)
\(S_{66}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}1.725 \times 10^5\)	\(\phantom{-}1.725 \times 10^5\)