Pipe

Probelm description

Figure 41 Cross section of the pipe [YU2005].

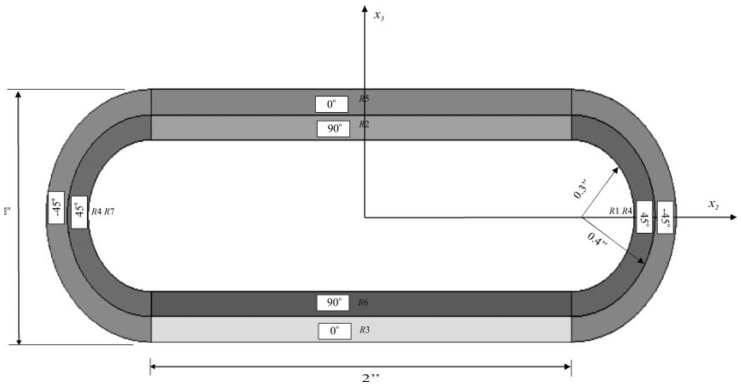
This example has the cross section as shown in Fig. 41 [YU2005]. This cross section has two straight walls and two half circular walls. \(r=1.0\) in. and other dimensions are shown in the figure. Each wall has the layup having two layers made from one material. Fiber orientations for each layer are also given in the figure. Material properties and layups are given in Table 17 and Table 18. Cross-sectional properties are given in Table 19 and compared with the results from [YU2005]. The tiny differences are due to different meshes. Complete input files can be found in examples\ex_pipe\, including pipe.xml, baselines.xml, materials.xml, and layups.xml.

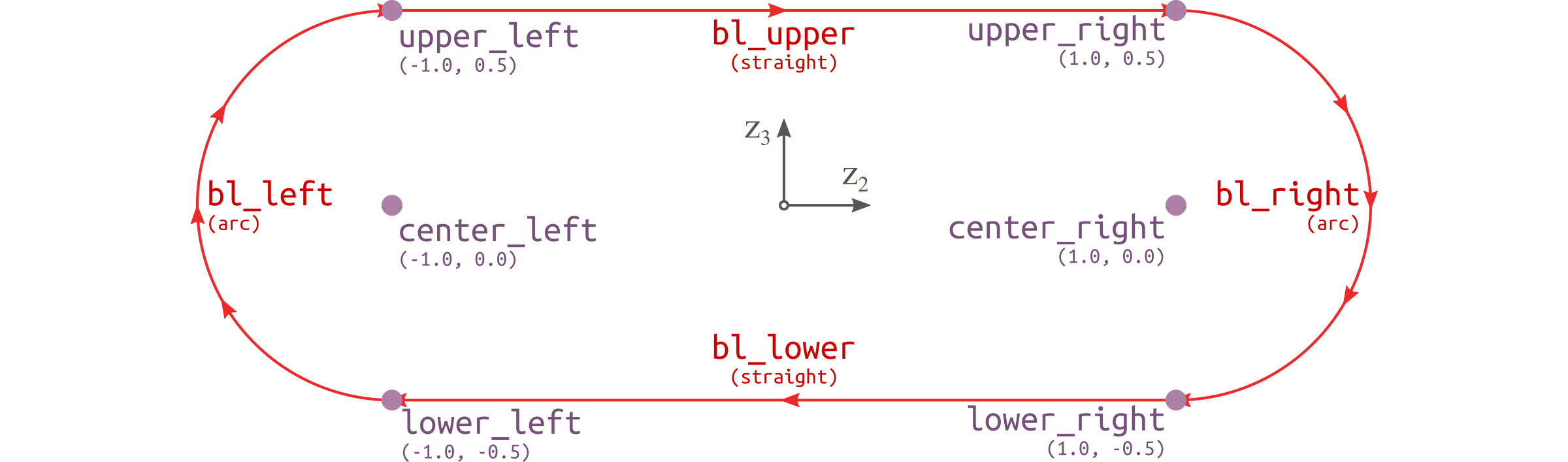
Figure 42 Base points and Base lines of the pipe cross section.

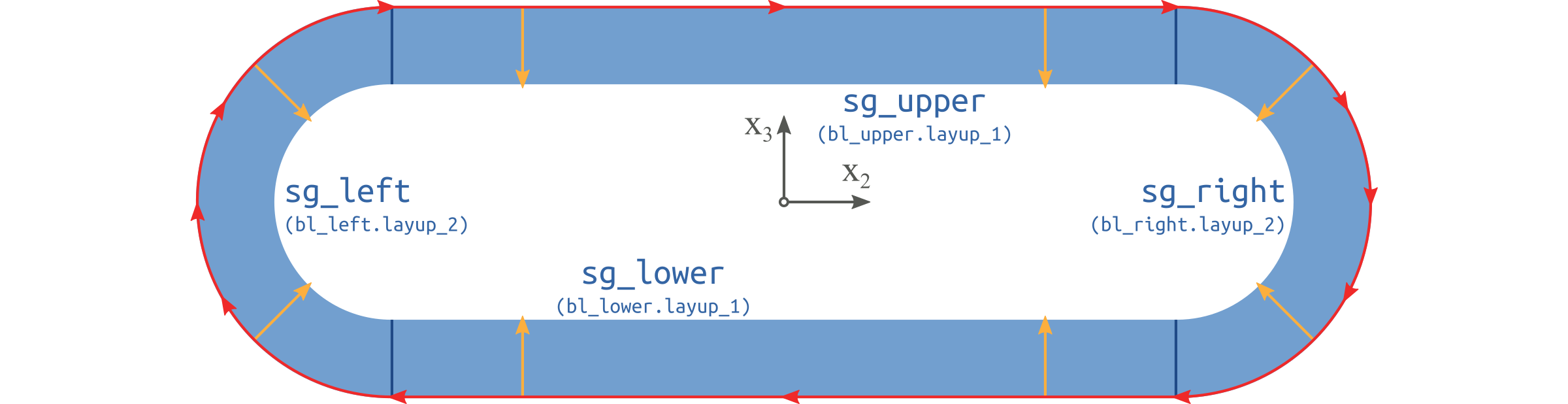
Figure 43 Segments of the pipe cross section.

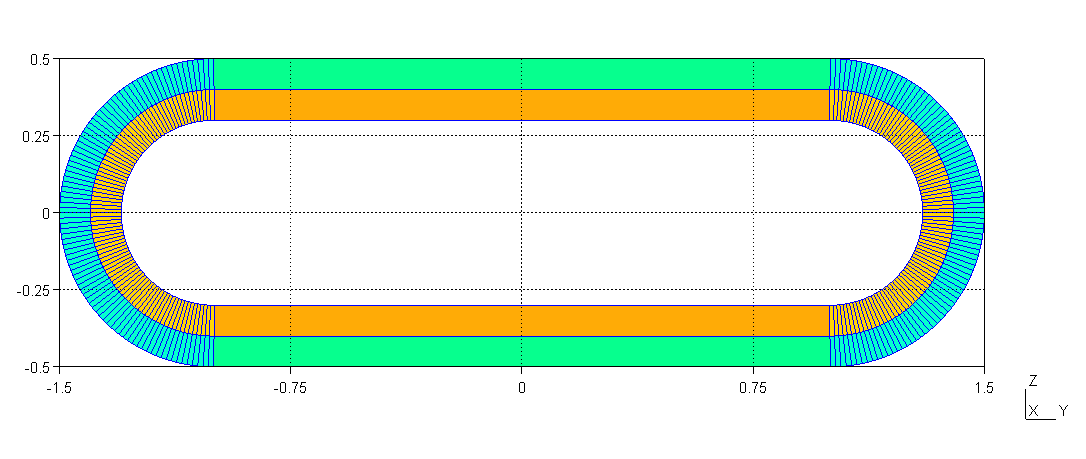
Figure 44 Meshed cross section viewed in Gmsh.

Table 17 Material properties

Name	Density	\(E_{1}\)	\(E_{2}\)	\(E_{3}\)	\(G_{12}\)	\(G_{13}\)	\(G_{23}\)	\(\nu_{12}\)	\(\nu_{13}\)	\(\nu_{23}\)
	\(\mathrm{lb\cdot sec^2/in^4}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)	\(10^6\ \mathrm{psi}\)
mat_1	0.057	20.59	1.42	1.42	0.87	0.87	0.87	0.42	0.42	0.42

Table 18 Layups

Name	Layer	Material	Ply thickness	Orientation	Number of plies
			\(\mathrm{in}\)	\(\circ\)
layup_1	1	mat_1	0.1	0	1
	2	mat_1	0.1	90	1
layup_2	1	mat_1	0.1	-45	1
	2	mat_1	0.1	45	1

Result

Table 19 Results

Component	Value	Reference [YU2005]
\(S_{11}\) [\(\mathrm{lbf}\)]	\(\phantom{-}1.03892 \times 10^7\)	\(\phantom{-}1.03890 \times 10^7\)
\(S_{22}\) [\(\mathrm{lbf}\)]	\(\phantom{-}7.85800 \times 10^5\)	\(\phantom{-}7.84299 \times 10^5\)
\(S_{33}\) [\(\mathrm{lbf}\)]	\(\phantom{-}3.31330 \times 10^5\)	\(\phantom{-}3.29002 \times 10^5\)
\(S_{14}\) [\(\mathrm{lbf \cdot in}\)]	\(\phantom{-}9.74568 \times 10^4\)	\(\phantom{-}9.82878 \times 10^4\)
\(S_{25}\) [\(\mathrm{lbf \cdot in}\)]	\(-8.02785 \times 10^3\)	\(-8.18782 \times 10^3\)
\(S_{36}\) [\(\mathrm{lbf \cdot in}\)]	\(-5.14533 \times 10^4\)	\(-5.18541 \times 10^4\)
\(S_{44}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}6.89600 \times 10^5\)	\(\phantom{-}6.86973 \times 10^5\)
\(S_{55}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}1.88230 \times 10^6\)	\(\phantom{-}1.88236 \times 10^6\)
\(S_{66}\) [\(\mathrm{lbf \cdot in^2}\)]	\(\phantom{-}5.38985 \times 10^6\)	\(\phantom{-}5.38972 \times 10^6\)